梯度下降

在这节课，我们将学习梯度下降算法背后的准则和数学原理。

梯度计算

在上几个视频中，我们了解到为了最小化误差函数，我们需要获得一些导数。我们开始计算误差函数的导数吧。首先要注意的是 s 型函数具有很完美的导数。即

\sigma'(x) = \sigma(x) (1-\sigma(x))

原因是，我们可以使用商式计算它：

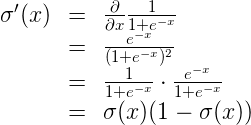
现在，如果有
m
个样本点，标为
x^{(1)}, x^{(2)}, \ldots, x^{(m)},
误差公式是：

E = -\frac{1}{m} \sum_{i=1}^m \left( y^{(i)} \ln(\hat{y^{(i)}}) + (1-y^{(i)}) \ln (1-\hat{y^{(i)}}) \right)

预测是
\hat{y^{(i)}} = \sigma(Wx^{(i)} + b).

我们的目标是计算
E,
在单个样本点 x
时的梯度（偏导数），其中 x 包含 n 个特征，即x = (x_1, \ldots, x_n),。

\nabla E =\left(\frac{\partial}{\partial w_1}E, \cdots, \frac{\partial}{\partial w_n}E, \frac{\partial}{\partial b}E \right)

为此，首先我们要计算，
\frac{\partial}{\partial w_j} \hat{y}.

因为这是上述公式里的第一个元素。

\hat{y} = \sigma(Wx+b),
因此：

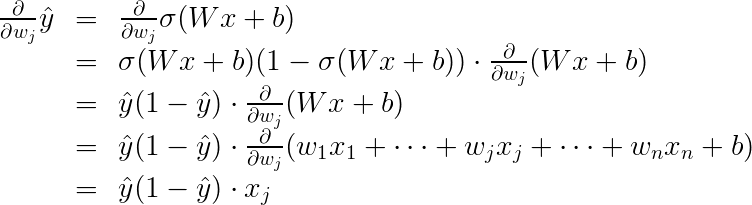
最后一个等式是因为和中的唯一非常量项相对于
w_j
正好是
w_j x_j,
明显具有导数
x_j.

现在可以计算
\frac {\partial} {\partial w_j} E

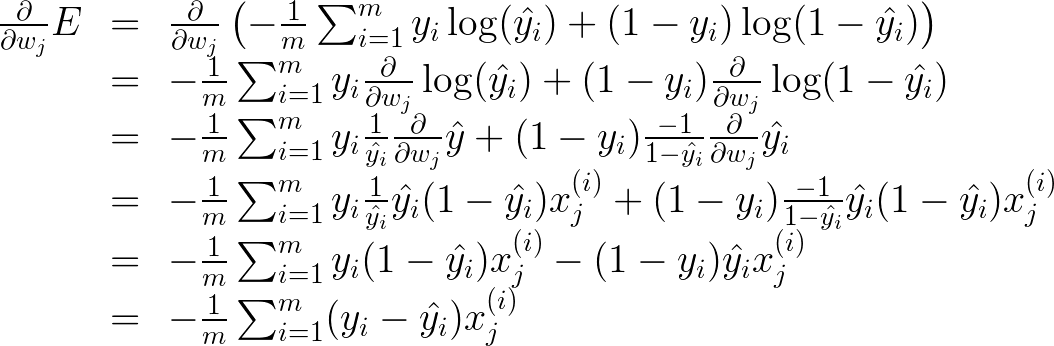
类似的计算将得出：（备注：下图公式缺少一个负号，且其为 m 个样本点时的公式）

【针对单个样本点时，E 对 b 求偏导的公式为：\frac {\partial} {\partial b} E=-(y -\hat{y})】

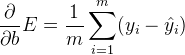
这个实际上告诉了我们很重要的规则。对于具有坐标
(x_1, \ldots, x_n),
的点，标签
y,
预测
\hat{y},
该点的误差函数梯度是
\left(-(y - \hat{y})x_1, \cdots, -(y - \hat{y})x_n, -(y - \hat{y}) \right).

总之

\nabla E(W,b) = -(y - \hat{y}) (x_1, \ldots, x_n, 1).

如果思考下，会发现很神奇。梯度实际上是标量乘以点的坐标！什么是标量？也就是标签和预测之间的差别。这意味着，如果标签与预测接近（表示点分类正确），该梯度将很小，如果标签与预测差别很大（表示点分类错误），那么此梯度将很大。请记下：小的梯度表示我们将稍微修改下坐标，大的梯度表示我们将大幅度修改坐标。

如果觉得这听起来像感知器算法，其实并非偶然性！稍后我们将详细了解。